출처 : https://o-tantk.github.io/posts/finding-median/
(감사합니다!)
중앙값 찾기
중앙값은 정렬된 배열에서 찾아야 한다. 가장 먼저 정렬을 수행해야 한다.정렬 후엔, 단순히 배열 크기의 절반에 해당하는 인덱스에 접근해 반환하면 된다.
실시간으로 중앙값(Running Median) 찾기
수행 속도가 훨씬 빠른, 추가/삭제가 정렬과 함께 이루어지는 자료 구조를 이용, Heap
(감사합니다!)
중앙값 찾기
중앙값은 정렬된 배열에서 찾아야 한다. 가장 먼저 정렬을 수행해야 한다.정렬 후엔, 단순히 배열 크기의 절반에 해당하는 인덱스에 접근해 반환하면 된다.
실시간으로 중앙값(Running Median) 찾기
수행 속도가 훨씬 빠른, 추가/삭제가 정렬과 함께 이루어지는 자료 구조를 이용, Heap
알고리즘
- Max heap은 최대값에 바로 접근할 수 있다.
- Min heap은 최소값에 바로 접근할 수 있다.
Heap의 두 성질 이용해, 중앙값보다 작은 값들은 Max heap에, 중앙값보다 큰 값들은 Min heap에 저장하는 방식으로 중앙값을 찾는 알고리즘을 구현할 수 있다. 아래의 상황을 보자.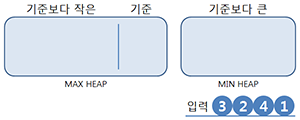 먼저, 작은 값과 큰 값을 나눌 기준이 필요하다. 중앙값이 아니라 굳이 기준이라 표현한 이유는, 개수가 짝수일 때를 고려해서이다.
먼저, 작은 값과 큰 값을 나눌 기준이 필요하다. 중앙값이 아니라 굳이 기준이라 표현한 이유는, 개수가 짝수일 때를 고려해서이다.
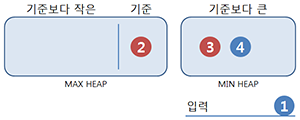
기준은 어차피 가운데에 있으니, 변수를 따로 만들 필요 없이 Max heap 또는 Min heap에 포함시키면 된다. 여기선 Max heap을 이용했다.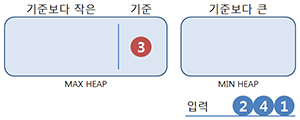 첫 번째 입력은 별 수 없이 기준이 된다. 홀수개이므로 중앙값은
첫 번째 입력은 별 수 없이 기준이 된다. 홀수개이므로 중앙값은
나머지는 기준보다 작다면 Max heap에, 크다면 Min heap에 넣는다. 그리고, Max heap과 Min heap의 크기가 균형되도록 조절한다. 다만, 기준을 고려해 기준을 가진쪽이 하나는 더 클 수 있도록 허용한다.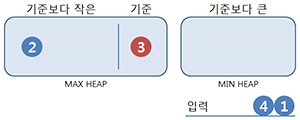
 먼저, 작은 값과 큰 값을 나눌 기준이 필요하다. 중앙값이 아니라 굳이 기준이라 표현한 이유는, 개수가 짝수일 때를 고려해서이다.
먼저, 작은 값과 큰 값을 나눌 기준이 필요하다. 중앙값이 아니라 굳이 기준이라 표현한 이유는, 개수가 짝수일 때를 고려해서이다.기준은 어차피 가운데에 있으니, 변수를 따로 만들 필요 없이 Max heap 또는 Min heap에 포함시키면 된다. 여기선 Max heap을 이용했다.
 첫 번째 입력은 별 수 없이 기준이 된다. 홀수개이므로 중앙값은
첫 번째 입력은 별 수 없이 기준이 된다. 홀수개이므로 중앙값은 3이다.나머지는 기준보다 작다면 Max heap에, 크다면 Min heap에 넣는다. 그리고, Max heap과 Min heap의 크기가 균형되도록 조절한다. 다만, 기준을 고려해 기준을 가진쪽이 하나는 더 클 수 있도록 허용한다.


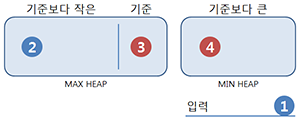
2는 기준보다 작으니 Max heap에 넣지만 균형을 맞추기 위해 Max heap의 최대값을 이동시킨다. 짝수개이므로 중앙값은 2와 3의 평균이다.

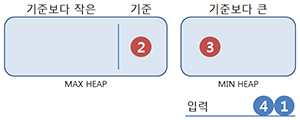
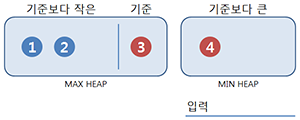
4는 기준보다 크니 Min heap에 넣지만 균형을 맞추기 위해 Min heap의 최소값을 이동시킨다. 홀수개이므로 중앙값은 3이다.

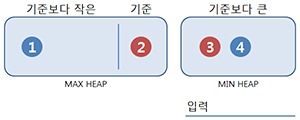
1은 기준보다 작으니 Max heap에 넣지만 균형을 맞추기 위해 Max heap의 최대값을 이동시킨다. 짝수개이므로 중앙값은 2와 3의 평균이다.입력이 들어올 때마다 한 번의 데이터 이동만으로 실시간으로 중앙값을 찾고 있다. Heap의 시간복잡도가
O(log N)이므로 최악의 경우라도 ‘삽입 + 삭제 + 삽입’의 O(3 log N)의 성능을 보인다.
댓글
댓글 쓰기